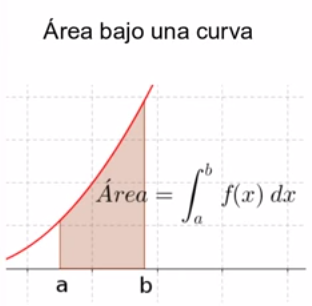
Sin embargo, hay veces en que la
curva tiene partes por debajo y partes por encima
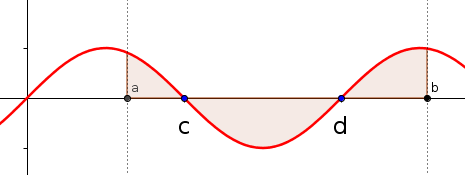
si hacemos la integral definida
entre a y b nos conduciría a un resultado erróneo. Habría que descomponer la
integral en tres partes correspondientes a los intervalos [a,c] [c,d] y [d,b] y
además tener en cuenta que en el intervalo [c,d] debemos tomar valor absoluto
(porque saldría un área negativa al estar por debajo del eje).
Lo más práctico es tomar valor
absoluto en todos los intervalos (y así no necesitamos saber los que están por
encima y los que están por debajo). El área (A) de la imagen anterior se
calcularía así:
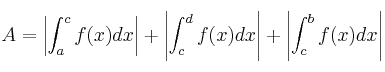
¿Cómo saber si la curva f(x) corta al eje X dentro del intervalo [a,b]?
Basta con resolver la
ecuación
Si al resolver la ecuación
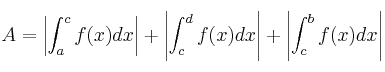

No hay comentarios:
Publicar un comentario