Este método de integración consiste en la aplicación de un
cambio de variable para simplificar el integrando. No vamos a explicar el
método formalmente, pero los pasos a seguir son los siguientes:
Escoger un cambio de variable z= función de x.
Despejar x para calcular dx.
Sustituir en la integral, resolverla y deshacer el cambio de
variable.
La dificultad del método es escoger un cambio útil, ya que,
en caso contrario, la integral resultante puede ser de mayor dificultad.
En la siguiente tabla se recogen los cambios de variable que
tienen alta probabilidad de funcionar en las integrales que usualmente veremos:
El método de cambio de variable es un poco más complicado
cuando se aplica en integrales definidas porque al cambiar la
variable, deben actualizarse los extremos de integración. Por
ejemplo, si los extremos de la integral inicial con variable x son 0
y 1 y la nueva variable es z=2x, entonces, los nuevos extremos serán 0 y
2. Una forma de evitar este problema es resolver primero la integral
indefinida.
EJEMPLO :
Integral de un cociente con exponenciales:
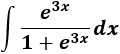
Atendiendo a la tabla, escogemos el cambio de variable
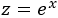
Con este cambio, , así que obtendremos un cociente de polinomios.
Despejamos aplicando logaritmos:
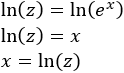
Derivamos para calcular (respecto de en el lado izquierdo y respecto de en el derecho):
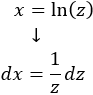
Sustituimos en la integral y simplificamos (no olvidéis sustituir también ):
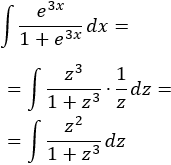
La integral obtenida es inmediata (un logaritmo):
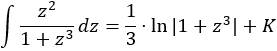
Deshacemos el cambio de variable:
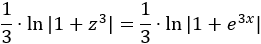
Por tanto,
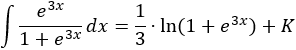
Nota: el valor absoluto ya no es necesario porque el argumento nunca es no positivo.
Integral
Integral de un cociente con raíz cuadrada en el denominador:
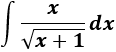
Escogemos el cambio de variable radicando para que desaparezca la raíz cuadrada:
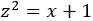
Despejamos y derivamos:
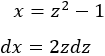
Sustituimos en la integral y simplificamos:
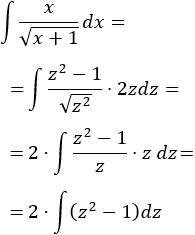
Calculamos la integral:
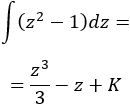
Deshacemos el cambio de variable:
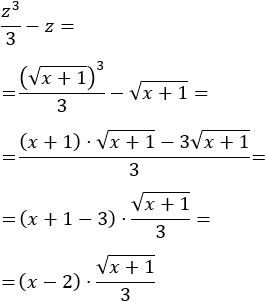
Por tanto,
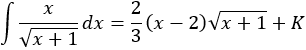


No hay comentarios:
Publicar un comentario