Definición 1 Se dice que una función racional P(x) /Q(x) es una fracción propia, si el grado del polinomio P(x) es menor que el grado del polinomio Q(x). En caso contrario, es decir, si el grado de P(x) es mayor o igual al de Q(x), la fracción se llama impropia.
Toda fracción impropia se puede expresar, efectuando la división, como la suma de un polinomio mas una fracción propia.
Es decir, P(x)/ Q(x) = {polinomio} + N1(x)/ Q(x)
Caso 1
El denominador q(x) es un producto de factores lineales distintos.
Esto significa que podemos escribir Q(x) = (a1x + b1)(a2x + b2)· · ·(akx + bk)
en donde no hay factor que se repita.
En este caso, existen constantes A1, A2, · · · , Ak tales que
Caso 2
El denominador q(x) es un producto de factores lineales, algunos de los cuales se repiten. Si Q(x) tiene un factor lineal repetido k veces de la forma (a1x + b1) k , entonces la descomposición en fracciones parciales contiene k términos de la forma:
Caso 3
El denominador q(x) contiene factores cuadráticos irreductibles, ninguno de los cuales se repite. Si Q(x) tiene un factor cuadrático no repetido de la forma ax2 + bx + c, en donde, b 2 − 4ac < 0, entonces la descomposición en fracciones parciales contiene un término de la forma:
El denominador q(x) contiene un factor irreductible repetido.
Si Q(x) tiene un factor cuadrático repetido k veces de la forma (ax2 + bx + c)
k
, donde
b
2 − 4ac < 0, entonces la descomposición en fracciones parciales contiene k términos de la
forma:

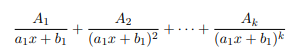



No hay comentarios:
Publicar un comentario