Diferencial de una función

Si  es una función derivable, la diferencial de una función correspondiente al incremento  de la variable independiente, es el producto .

La diferencial de una función se representa por  ó .

Ejemplos

Hallar las diferenciales de las siguientes funciones: 

a) y =  3x     

  dy = 3 dx  //resp.

b)  y =  3x⁴     

      dy = 12x³  dx  //resp

c)  y = cos 3x  

      dy = (- 3sen 3x) dx // resp

      dy = (- 3sen 3x) dx // resp

Sumas de Riemann

 

La integral de Riemann se define en términos de Sumas de Reimann de funciones respecto de particiones etiquetadas de un intervalo. 

Sea [a,b] un intervalo cerrado de la recta real; entonces una partición etiquetada de [a,b] es una secuencia finita  y denotamos la partición como  Esto divide al intervalo  en  subintervalos , cada uno de los cuales es "etiquetado" con un punto especificado t_i de . Sea Δ_i = x_i−x_i−1 la anchura del subintervalo i; el paso de esta partición etiquetada es el ancho del subintervalo más grande obtenido por la partición, max_i=1…n Δ_i. Un sumatorio de Riemann de una función f respecto de esta partición etiquetada se define como

${\displaystyle \sum _{i=1}^{n}f(t_{i})\Delta _{i};}$

Así cada término del sumatorio es el área del rectángulo con altura igual al valor de la función en el punto especificado del subintervalo dado, y de la misma anchura que la anchura del subintervalo. La integral de Riemann de una función ${\displaystyle f}$ sobre el intervalo ${\displaystyle [a,b]}$ es igual a S si:

Para todo  existe  tal que, para cualquier partición etiquetada  con paso más pequeño que δ, se tiene

${\displaystyle \left|S-\sum _{i=1}^{n}f(t_{i})\Delta _{i}\right|<\varepsilon }$, donde ${\displaystyle S=\int _{a}^{b}f=\lim _{\|{\Delta _{i}}\|\to 0}\sum _{i=1}^{n}f(t_{i})\Delta _{i}}$

Cuando las etiquetas escogidas dan el máximo (o mínimo) valor de cada intervalo, el sumatorio de Riemann pasa a ser un sumatorio de Darboux superior (o inferior), lo que sugiere la estrecha conexión que hay entre la integral de Riemann y la integral de Darboux.

Interpretación geométrica

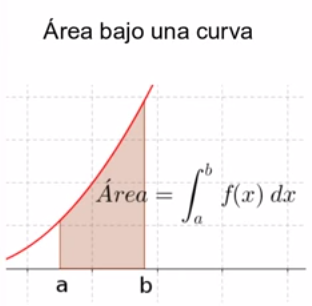
En Análisis real, la integral de Riemann es una forma simple de definir la integral de una función sobre un intervalo como el área localizada bajo la curva de la función.

Sea ${\displaystyle f}$ una función con valores reales definida sobre el intervalo ${\displaystyle [a,b]}$, tal que para todo ${\displaystyle x}$, ${\displaystyle f(x)\geq 0}$ (es decir, tal que ${\displaystyle f}$ es positiva).

Sea ${\displaystyle S_{f}=\{(x,y)|0\leq y\leq f(x)}$ la región del plano delimitada por la curva correspondiente a la función ${\displaystyle f}$, el eje de las abscisas y las rectas verticales de ecuaciones ${\displaystyle x=a}$ y ${\displaystyle x=b}$. Estamos interesados en medir el área del dominio ${\displaystyle S}$, si es que se puede medir.

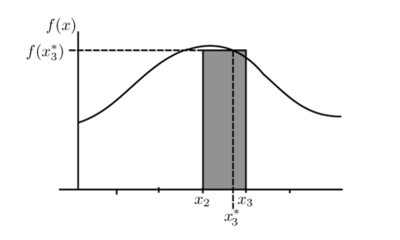
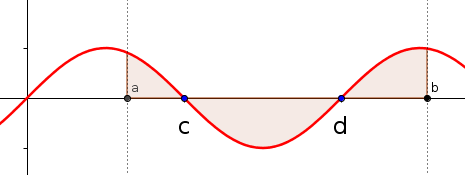
Para obtener una aproximación al área encerrada debajo de una curva, se la puede dividir en rectángulos como indica la figura.

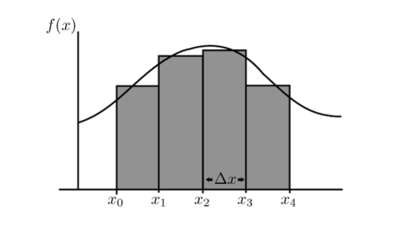
El área de cada rectángulo, es el producto de la función en un punto, por el ancho del intervalo.

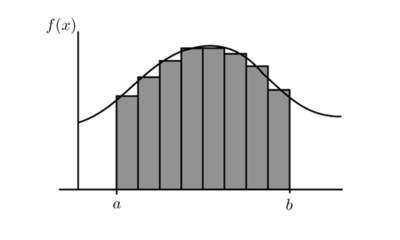
Al aumentar el número de rectángulos se obtiene una mejor aproximación.

Área Bajo la Curva

La interpretación geométrica de la regla de Barrow nos dice que la integral definida representa el área entre la curva y el eje de abcisas

 Esto es cierto si la curva es positiva en el intervalo [a,b], es decir, si está por encima del eje OX.
 Si estuviese por debajo, nos saldría un resultado negativo (tomando valor absoluto se soluciona el problema).

Sin embargo, hay veces en que la curva tiene partes por debajo y partes por encima

si hacemos la integral definida entre a y b nos conduciría a un resultado erróneo. Habría que descomponer la integral en tres partes correspondientes a los intervalos [a,c] [c,d] y [d,b] y además tener en cuenta que en el intervalo [c,d] debemos tomar valor absoluto (porque saldría un área negativa al estar por debajo del eje).

Lo más práctico es tomar valor absoluto en todos los intervalos (y así no necesitamos saber los que están por encima y los que están por debajo). El área (A) de la imagen anterior se calcularía así:

¿Cómo saber si la curva f(x) corta al eje X dentro del intervalo [a,b]?

Basta con resolver la ecuación   f(x) = 0 y ver si alguna de las soluciones está dentro del intervalo [a,b].

Si al resolver la ecuación  f(x) = 0 obtenemos que entre las soluciones hay dos (c y d) dentro del intervalo, calcularíamos el área con la fórmula:

Notación Sumatoria

 La sumatoria o sumatorio (llamada también notación sigma ) es una operación matemática que se emplea para calcular la suma de muchos o infinitos sumandos.

La operación sumatoria se expresa con la letra griega sigma mayúscula Σ, y se representa así:

Expresión que se lee: " sumatoria de Xi,  donde i toma los valores desde 1 hasta n ".

i es el valor inicial, llamado límite inferior.

n es el valor final, llamado límite superior.

Pero necesariamente debe cumplirse que:

i ≤ n

Si la sumatoria abarca la totalidad de los valores, entonces no se anotan sus límites y su expresión se puede simplificar:

Si se quiere expresar la suma de los cinco primeros números naturales se puede hacer de esta forma:

Integral definida e indefinida

INTEGRAL DEFINIDA

Si f es una función definida en el intervalo cerrado [a,b], entonces la integral definida de f de a a b se define como:

 (si el límite existe)

 f (x) se llama integrando.

a y b son los extremos o límites de integración ( a es el extremo inferior y b es el extremo superior) 

∫ se llama signo de integración. 

Si ∆ →0 implica que n→∞, por lo tanto:

PROPIEDADES DE LA INTEGRAL DEFINIDA

 Si f (x) y g(x) son dos funciones continuas en el intervalo de integración [a, b] y k una constante cualquiera:

INTEGRAL INDEFINIDA O ANTIDERIVADA

 Una función F será antiderivada, o primitiva, de otra función f en un intervalo [a,b] si F'(x) = f (x) para todo valor de x en el intervalo.  

Esto es, si 

Ejemplo. 

Sea f (x)= 5x³ + 12x² -10x.

 Eso implica: f'(x ) 15x² + 24x -10  

 La antiderivada de esta función es la función original f (x). 

Esto significa que 

∫ (15x² + 24x −10) dx = 5x³ + 12x² -10x.

La función f (x) tiene una antiderivada particular [a,b] que es F(x). 

La antiderivada general de f (x) es: 

F(x) + C   donde C es una constante.  

 

Método de Integración por sustitución trigonométrica

En la sustitución trigonométrica consiste en la sustitución de determinadas expresiones mediante el uso de funciones trigonométricas. En cálculo, la sustitución trigonométrica es una técnica que permite evaluar integrales, puesto que se pueden utilizar identidades trigonométricas para simplificar ciertas integrales que contienen expresiones radicales.

Fórmula general

La integración por sustitución trigonométrica sirve para integrar funciones que tienen la siguiente forma:

, ${\displaystyle {\sqrt {a^{2}+u^{2}}}}$ y ${\displaystyle {\sqrt {u^{2}-a^{2}}}}$

Este método se basa en el uso de determinadas propiedades de los triángulos rectángulos, como el teorema de Pitágoras y ciertas identidades trigonométricas.

En el caso general, la integral a resolver es:

Simplificando paso a paso el término de la raíz, en primer lugar se saca ${\displaystyle A}$ como factor común, y luego se opera para poder dejarlo como suma de cuadrados:

Si se agrupan los coeficientes de esta forma,

${\displaystyle m^{2}=A}$

${\displaystyle a^{2}=C-{\frac {B^{2}}{4A}}}$

se obtendrá una de estas tres situaciones posibles:

1. ${\displaystyle A<0}$ y ${\displaystyle C-{\frac {B^{2}}{4A}}>0}$ es decir: ${\displaystyle {\sqrt {a^{2}-m^{2}\left(x+{\frac {B}{2A}}\right)^{2}}}}$
2. ${\displaystyle A>0}$ y ${\displaystyle C-{\frac {B^{2}}{4A}}>0}$ es decir: ${\displaystyle {\sqrt {a^{2}+m^{2}\left(x+{\frac {B}{2A}}\right)^{2}}}}$
3. ${\displaystyle A>0}$ y ${\displaystyle C-{\frac {B^{2}}{4A}}<0}$ es decir: ${\displaystyle {\sqrt {m^{2}\left(x+{\frac {B}{2A}}\right)^{2}-a^{2}}}}$

Ahora, haciendo que:

${\displaystyle u=m\left(x+{\frac {B}{2A}}\right)}$

se obtiene una de las tres formas de radicales conocidas. Los cambios que hay que realizar entonces según cada situación son los siguientes:

1. ${\displaystyle {\sqrt {a^{2}-u^{2}}};\quad u=a\operatorname {sen}(t)}$
2. ${\displaystyle {\sqrt {a^{2}+u^{2}}};\quad u=a\tan(t)}$
3. ${\displaystyle {\sqrt {u^{2}-a^{2}}};\quad u=a\sec(t)}$

La integral de esta forma, se transforma en una integral trigonométrica en ${\displaystyle t}$. Una vez resuelta, se deshace el cambio.

Ejemplo I

Considérese la integral definida

${\displaystyle \int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx}$

que puede ser evaluada haciendo el cambio de variable

${\displaystyle {\begin{aligned}x&=2\operatorname {sen} \theta \\dx&=2\cos \theta \,d\theta \end{aligned}}}$

y en este caso, los límites de integración estarán determinados por

${\displaystyle \theta ={\text{arcsen}}\left({\frac {x}{2}}\right)}$

Tenemos que

si ${\displaystyle x=-1}$ entonces ${\displaystyle \theta ={\text{arcsen}}\left(-{\frac {1}{2}}\right)=-{\frac {\pi }{6}}}$

y si ${\displaystyle x=1}$ entonces ${\displaystyle \theta ={\text{arcsen}}\left({\frac {1}{2}}\right)={\frac {\pi }{6}}}$

entonces

${\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\int _{-\pi /6}^{\pi /6}{\sqrt {4-4\operatorname {sen} ^{2}\theta }}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(1-\operatorname {sen} ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(\cos ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}(2\cos \theta )(2\cos \theta )\,d\theta \\[6pt]&=4\int _{-\pi /6}^{\pi /6}\cos ^{2}\theta \,d\theta \\[6pt]&=4\int _{-\pi /6}^{\pi /6}\left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\[6pt]&=2\left[\theta +{\frac {1}{2}}\operatorname {sen} 2\theta \right]_{-\pi /6}^{\pi /6}\\[6pt]&=[2\theta +\operatorname {sen} 2\theta ]{\Biggl |}_{-\pi /6}^{\pi /6}\\[6pt]&=\left({\frac {\pi }{3}}+\operatorname {sen} {\frac {\pi }{3}}\right)-\left(-{\frac {\pi }{3}}+\operatorname {sen} \left(-{\frac {\pi }{3}}\right)\right)\\[6pt]&={\frac {2\pi }{3}}+{\sqrt {3}}\end{aligned}}}$

Por otro lado, si aplicamos directamente los límites de integración para la fórmula de la antiderivada obtenemos

${\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\left[2\;{\text{arcsen}}\left({\frac {x}{2}}\right)+{\frac {x}{2}}{\sqrt {4-x^{2}}}\right]_{-1}^{1}\\[6pt]&=\left(2\;{\text{arcsen}}\left({\frac {1}{2}}\right)+{\frac {1}{2}}{\sqrt {3}}\right)-\left(2\;{\text{arcsen}}\left(-{\frac {1}{2}}\right)-{\frac {1}{2}}{\sqrt {3}}\right)\\[6pt]&=\left(2\cdot {\frac {\pi }{6}}+{\frac {\sqrt {3}}{2}}\right)-\left(2\cdot \left(-{\frac {\pi }{6}}\right)-{\frac {\sqrt {3}}{2}}\right)\\[6pt]&={\frac {2\pi }{3}}+{\sqrt {3}}\end{aligned}}}$